Implementation for Planning in Generalized Belief Space (GBS)

Matlab implementation of an active-perception planner that plans uncertainty-reducing behaviors.

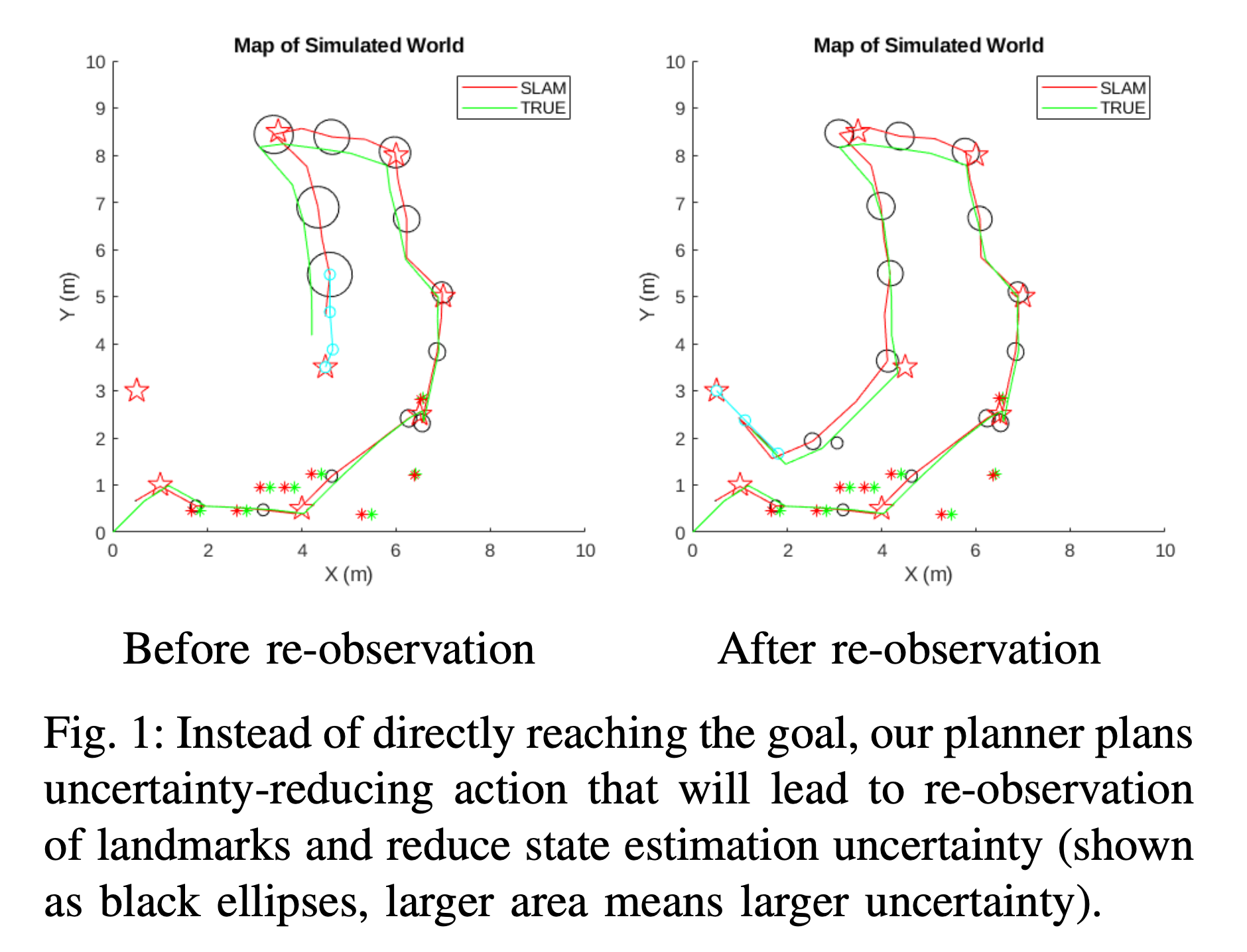
This project is done as our class project for CMU 16-748 Underactuated Robotics.

Authors

• Haowen Shi (haowensh@andrew.cmu.edu)
• Hans Kumar (hansk@andrew.cmu.edu)

Abstract

Belief Space Planning has been of interest in the robotics community because of its ability to take into account robot state uncertainty during planning. [1] presented a method for planning in the belief space given a known map by assuming maximum likelihood observations. [2] extended this work to support Active SLAM tasks by introducing the concept of the generalize belief space (GBS), which contains a joint belief state consisting of the robot state and the world state. By planning in the GBS, no prior knowledge of the map is required to perform planning. This is useful for autonomous exploration tasks such as confined space inspection, etc. where the robot has to plan uncertainty-reducing actions to improve localization accuracy while fulfilling planning objectives. In this project we implement [2] from scratch and evaluate its performance against a naive LQR controller on several different simulated maps.

Implementation Details

High Level Overview

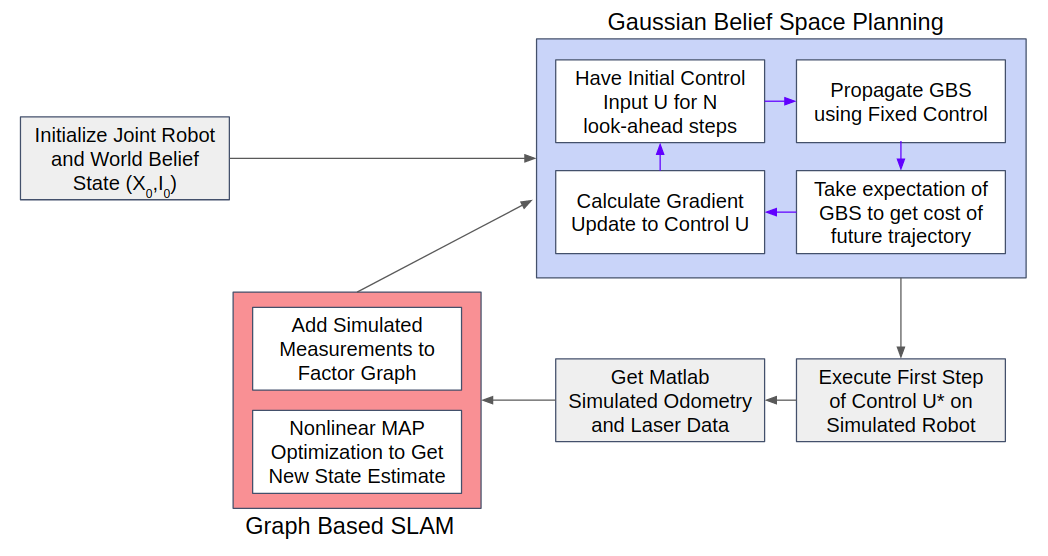
The original authors argued that planning and perception should be closely coupled. The red group contains the perception / state-estimation components and the blue group contains the planning components. For state-estimation we use a factor-graph based optimization implemented using the GTSAM library; for planning we implemented the dual-layer optimization process from sctratch based on [2].

Results

We evaluate the performance of our planner on three maps: Closure, Oasis and Uniform.

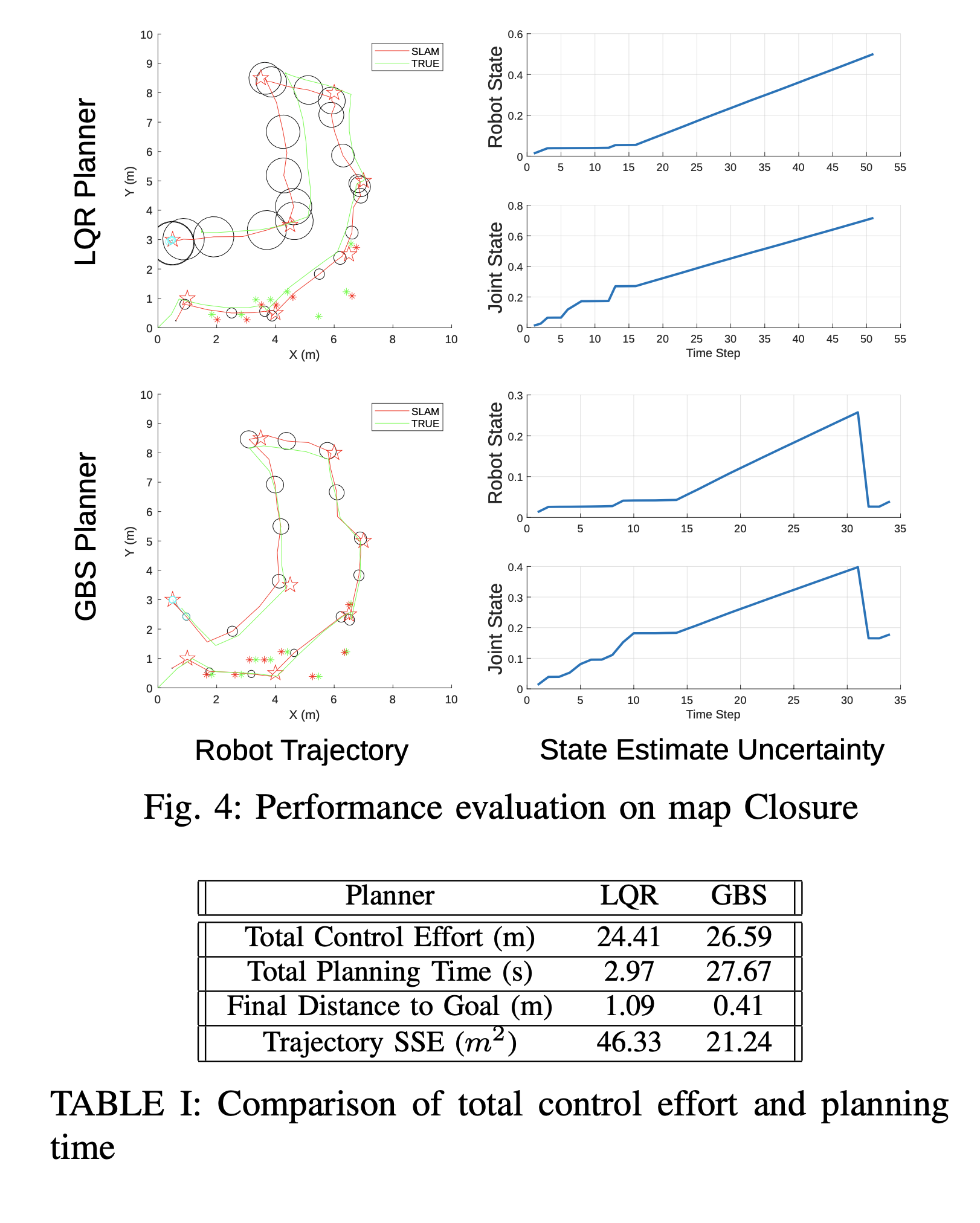Fig. 4 show the trajectory visualization and evolution of uncertainty for the LQR planner and our GBS planner respectively in the map called Closure. The black ellipses in the figures represent the uncertainty in the robot state estimate, where a bigger ellipse means higher uncer- tainty. The naive LQR planner does not take uncertainty into account while planning so, over the entire trajectory, state estimate uncertainty keeps growing. On the other hand, our GBS planner can steer towards prior observed landmarks to actively reduce uncertainty. The bottom right of Fig. 4 shows the sharp decrease in state estimate uncertainty after re- observation of landmarks due to the control actions produced by the GBS planner. This map demonstrated that our GBS controller is able to reach the final landmark with a much higher precision than LQR controller, as shown in table I. The total control effort of the GBS planner is greater than that of the LQR planner because of the extra path travelled to re-observe landmarks, which is expected and acceptable. However, the total planning time of the GBS planner is one order of magnitude higher than LQR because of the computation overhead from iterative optimization.

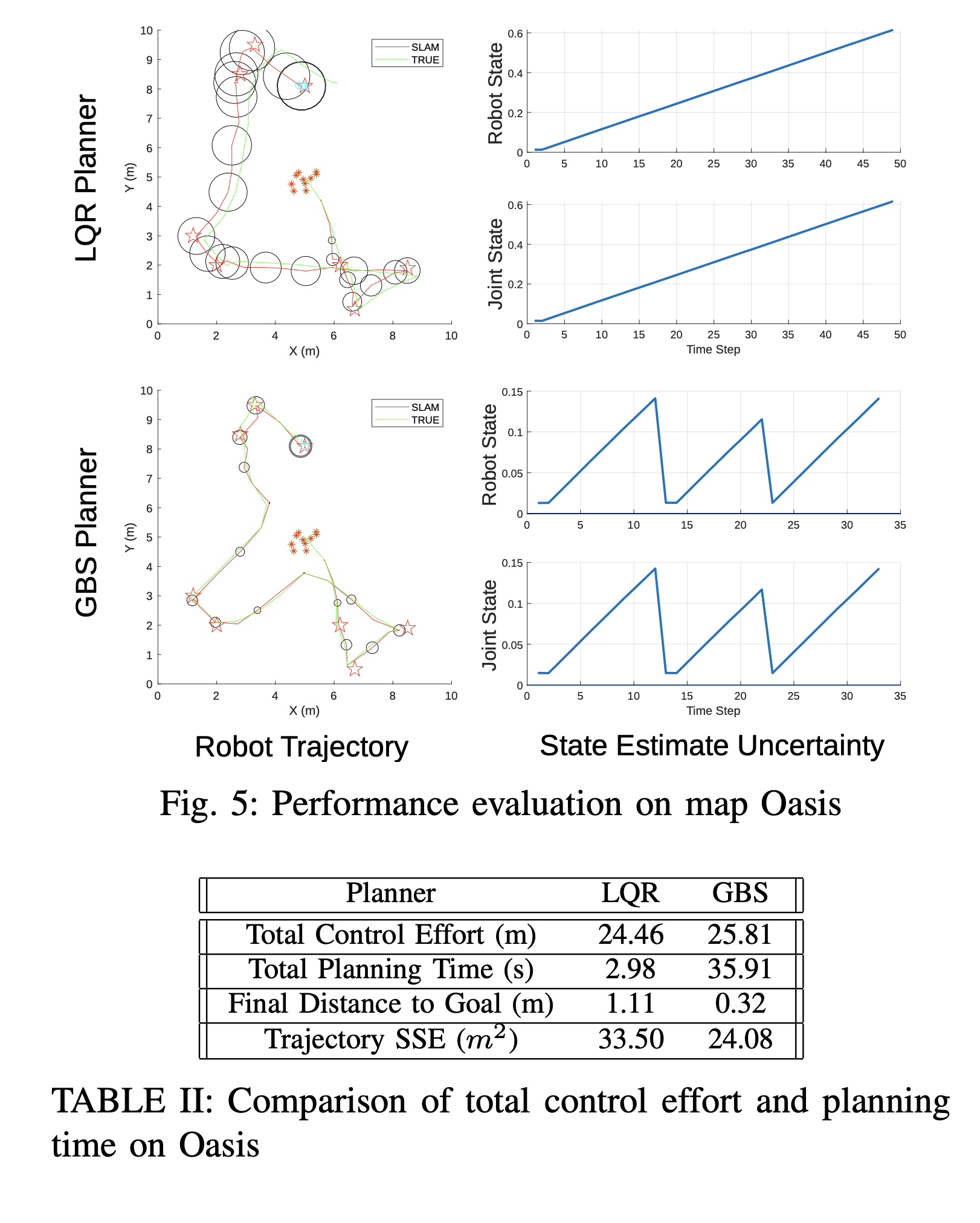Fig. 5 shows that the GBS planner goes out of the way to move toward the center of the map on two occasions in order to reduce the uncertainty of the robot. The group of landmarks in the center of the map serves as a uncertainty reducing location for the robot to travel to whenever the uncertainty grows to high. Compared to LQR method, the GBS method was able to reach the final goal position with much less overall uncertainty and position error. Table II shows that this increase in goal reaching accuracy comes at the cost of slightly higher control effort and much higher planning time.

On the Uniform map, Fig. 6 shows the GBS planner does nothing out of the ordinary compared to the LQR method. This is expected because the robot is almost always able to observe landmarks to suppress uncertainty, so the shortest path objective dominates the cost function. Even so, the GBS planner has better performance than the LQR planner in terms of uncertainty and final position error shown in Table III. We believe that this increase in performance is because the GBS planner is taking less control actions. By taking less control actions, the overall uncertainty of the state also grows less.

Report

Here’s a more complete report on this implementation work.

References

[1] R. PlattJr, R. Tedrake, L. Kaelbling, and T. Lozano-Perez, “Belief space planning assuming maximum likelihood observations,” 2010.

[2] V. Indelman, L. Carlone, and F. Dellaert, “Planning in the continuous domain: A generalized belief space approach for autonomous navigation in unknown environments,” The International Journal of Robotics Research, vol. 34, no. 7, pp. 849–882, 2015.

[3] L. P. Kaelbling, M. L. Littman, and A. R. Cassandra, “Planning and acting in partially observable stochastic domains,” Artificial intelligence, vol. 101, no. 1-2, pp. 99–134, 1998.